Secrets…

Sora (of Sketchbook) has a Secret Skill:

Recently, I stumbled on to an anime trailer on YouTube that I’d watched ages ago:

Scrapped Princess Trailer

I’d call it a beautiful anime based on the vague memories of it that remain in my brain and am deeply amused at the words of ‘Scrapped Princess’ at the end of the trailer:

Apparently, the world would be a lot better off without me. … Never mind that! Let’s have tea…

Now that is some great combination of Inferiority & Superiority complexes. Anyway, want to know more names of amusing, brilliant, charming, delightful, engaging, fantastic, great, humorous, incredible, joyous, kinky, lovely, macabre, nice, outstanding, pointless, quirky, remarkable, serene, tasteful, unique, valuable, whimsical, xenophobic, youthful and zestful Manga / Anime? Head over to

My Hobbies

Splitting and Joining

There is a popular phrase describing hairs: split ends. But I guess they are referring only to the free-flowing ends of the hairs, which is what most people are worried about! Well, I say they should worry about both ends of their hairs:

That takes care of the first half of the title. Now, on to the second half where I will rant about

POLORAMA GENERATOR

, its origin and so on. As you might have noticed, ‘Polorama’ is a portmanteau constructed from ‘Polar’ & ‘Panorama’. So, the origin of this program is simple enough to imagine: I saw one of these and wanted to make one myself! That was about two years ago. An attempt at that time got me to something GUIless like

v0.0 Release 0 (2009) which produced images with interesting fractal patterns:

Obviously, I was doing something wrong [(x,y)⇒(r,θ)] and thought I’d need to come up with an algorithm to average surrounding colors and put those on the ‘remaining’ white pixels to get a ‘proper’ image. Let me just say that this strategy is for morons. I realized this fact (thanks to an ‘out-of-context’ statement from PJ) which has led us now to

v1.0 Release 1 (2011) where I use a much simpler algorithm of just mapping (r,θ)⇒(x,y)! This gives us a proper polorama of galaxy M83:

Also, here are some of the poloramas I made. Oh! I should also show you how the GUI of this version looks here, right? Wrong. For that, visit

POLORAMA GENERATOR 1.0.π Release 1

Straightening

Don’t you just love it when something does more than what it is supposed to do? Well, obviously, not in all cases or contexts but definitely in the one being discussed here!

This is what has happened above! Find out what else is possible at

Hugin – Panorama Photo Stitcher

Since You’ve been Gone, I’ve been Alone

Since you’ve been gone, I’ve been alone
Like an arm without a bone
Dangling limply like a phone that’s out of charge
Like Homer without Marge
Like an egg without a spoon
Like a dugong on the Moon
Like a clownfish without Nemo
Like Twilight without Emo
Like Hardy without Laurel
Like high ground without the moral
Like Disney without Walt
Like battery without assault
Like a pet shop without gerbils
Like Hitler without Göbbels
Running naked through a wedding
Driving fast, way out past Reading
Children slaughter kittens, playing with a nail gun…
Children’s laughter, kittens playing, Withnail and I, gone are these pleasures
Like a dilemma without the di
Just a lemma and a sigh
Like déjà without vu
I am nothing without you
Till the day that you come back
I’m like Whitney without crack.
-Bill Bailey (Dandelion Mind)

More Ramblings

Moving on…

In this post, I’m going to rant about

SUDOKU SOLVER

, its origin, appearance and functionalities. The idea for SS originated in my head after Shantanu tried to teach me (well, I did ask him!) how to solve a Sudoku. It was during one of the CMP Lab hours of Autumn’05 before Puja holidays. He taught me a ‘human’ variant of the logic ‘Deduction & Reduction’ apart from looking for ‘Single Possibilities’ as described later.

It seemed to me that these ‘Logics’ could be coded and a logical Sudoku Solver made, which would mimic how ‘I’ would solve one! I thought about this quite a lot over the holidays and even came up with two more Logics ‘Deduction from doublets’ & ‘Reduction to doublets’. Later, these were generalized to ‘Deduction from Multi-sets’ & ‘Reduction to Multi-sets’. Two more logics ‘Deduction from Num-Grids’ & ‘Deduction from Num-Chains’ were added subsequently. Each Logic is assigned a number (like 3 for SP) which are summed, depending on ‘how much’ Logic goes into solving, to give a Sudoku its numerical score and  assign one of the ten difficulty levels: ‘Easiest’, ‘V. Easy’, ’Easy’, ‘Below Average’, ‘Average’, ‘Above Average’, ‘Hard’, ‘V. Hard’, ‘Hardest’ & ‘Out of the World’.

I decided that the major version number should reflect the number of Logics coded and the minor version should reflect… my Whim! The GUI for SS has remained the same since its inception. Though, the three menus (‘File’, ‘Tools’ & ‘Help’) have gained a few additions over time. Have a look at the oldest & the newest GUI:

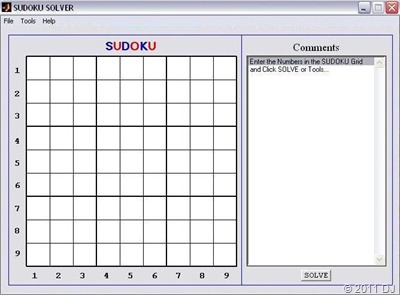
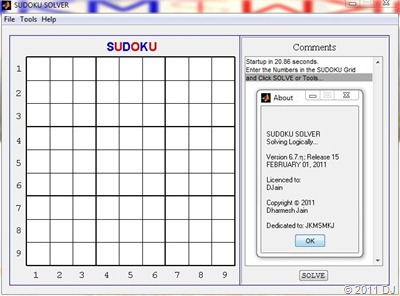
You can obviously Solve a Sudoku Completely but even Partially, which basically displays all the possibilities of individual (≤ 81) cells! However, there is no option of interrupting the (complete) solver and demanding the ‘partial’ results. (It is a Solver not a Trainer!) At first, I thought of not adding a Brute Force Algorithm but the graphics aspect of updating numbers while the recursive algorithm ran led me to include it! I also included an option ‘Use Logic’ but it can not be unchecked by usual means! The most latest addition is Speech Recognition, which allows one to input numbers by speaking them out loud as seen in this video:

SS 6.6 Demo

SS features a silly ‘security’ feature which supposedly prevents one from running the executable file of one computer on another! SS also asks for your name on the very first start to ‘license’ the program to you, which is displayed in ‘About SS’. It also saves the last Sudoku you solved for easy retrieval apart from providing usual functions like ‘Import’ & ‘Save’. You can also ‘Print’ the current screen to a .jpg file or a MATLAB figure. A Help file (accessible via ‘SS Know-How’) is included with the program along with a link to this post via ‘Learn SS Logic’. The latest release also has ‘Update’ & ‘Uninstall’ options!

This blog post will take place of the earlier Logic.pdf file as I link to the Site, which has an extensive collection of Logics used in Solving a Sudoku. The names (& possibly the implementation) of the ‘Strategies’ on that site differ from the names of the Logics in my Solver! In what follows, I’ll point out the many-to-one correspondence of the Strategies (30 excluding the Uniqueness & Trial and Error strategies) and Logics (6) below in [square brackets].

v1.0; Release 0 (2005) Single Possibilities [1, 2]

The simplest logic: Fill-in the single possibility for the particular cell! It can be represented in 4 ways:

Cell(R,C):N => Only no. (Abs. [Row, Col., Squ.])

R stands for Row (vertical numbers), C stands for Column (horizontal numbers) & N stands for the number filled in the specified cell.

v2.0; Release 0 (2005) Deduction & Reduction [6, 7]

Again 4 representations are possible here:

Squ.[sR,sC] & Row [Col.] R [C]: N =>
N removed from Row [Col.] R [C]

Row [Col.] R [C] & Squ.[sR,sC]: N =>
N removed from Squ.[sR,sC]

v3.0; Release 1 (2005) Reduction to Multi-sets [4]

3 representations are possible corresponding to 2, 3 or 4-sets. Sample shown for a 2-sets (doublet):

Cell(R₁,C₁) Cell(R₂,C₂): D₁ D₂ =>
N₁[N₂…] removed from Cell(R₁,C₁)
[M₁… removed from Cell(R₂,C₂)]

v4.x(0≤x≤9); Release 2-4 (2005-06) Deduction from Multi-sets [3, 5]

9 representations are possible ([2,3,4-sets]x[R,C,S]) here. A sample for doublet x R looks like:

Cell(R,C₁) Cell(R,C₂): D₁ D₂ =>
D₁ removed from Row R
[D₂ removed from Row R]

v5.x(0≤x≤5); Release 5-9 (2006-09) Deduction from Num-Grids [8, 11, 15]

6 representations are possible ([2,3,4-grids]x[R,C]) here. A sample for 2-grids x C looks like:

Cols(C₁,C₂) & Rows(R₁,R₂): G =>
G removed from Col.C₁ & Row(s):R₃[R₄…]
[G removed from Col.C₂ & Row(s):R₃…]

v6.x(2≤x≤7); Release 10-15 (2009-∞) Deduction from Num-Chains [9, 14]

4 representations are possible here:

NC – Type Ia:
N in Cells:(,) (,) […] &
N removed from Cells:(,) (,) […]

NC – Type Ib:
N in Cells:(,) (,) […] &
(,) […] =>
N removed from Cell(s):(,) […]

NC – Type IIa:
N in Cells:(,) (,) […] &
(,) […] with
N in Cell(s):(,) […] &
N removed from Cell(s):(,) […]

NC – Type IIb:
N in Cells:(,) (,) […] &
(,) […] with
N in Cells:(,) […] &
(,) […] =>
N removed from Cell(s):(,) […]

That makes a total of 12 out of 30 Strategies in SS, not bad, not bad at all! I’ve wanted to implement Y-Wing [10] & its generalizations [13, 18], which overlap with APE [19] for a long time but I guess that won’t happen in the near future. Anyway, I end this rather long post with

SUDOKU SOLVER 6.7.η Release 15